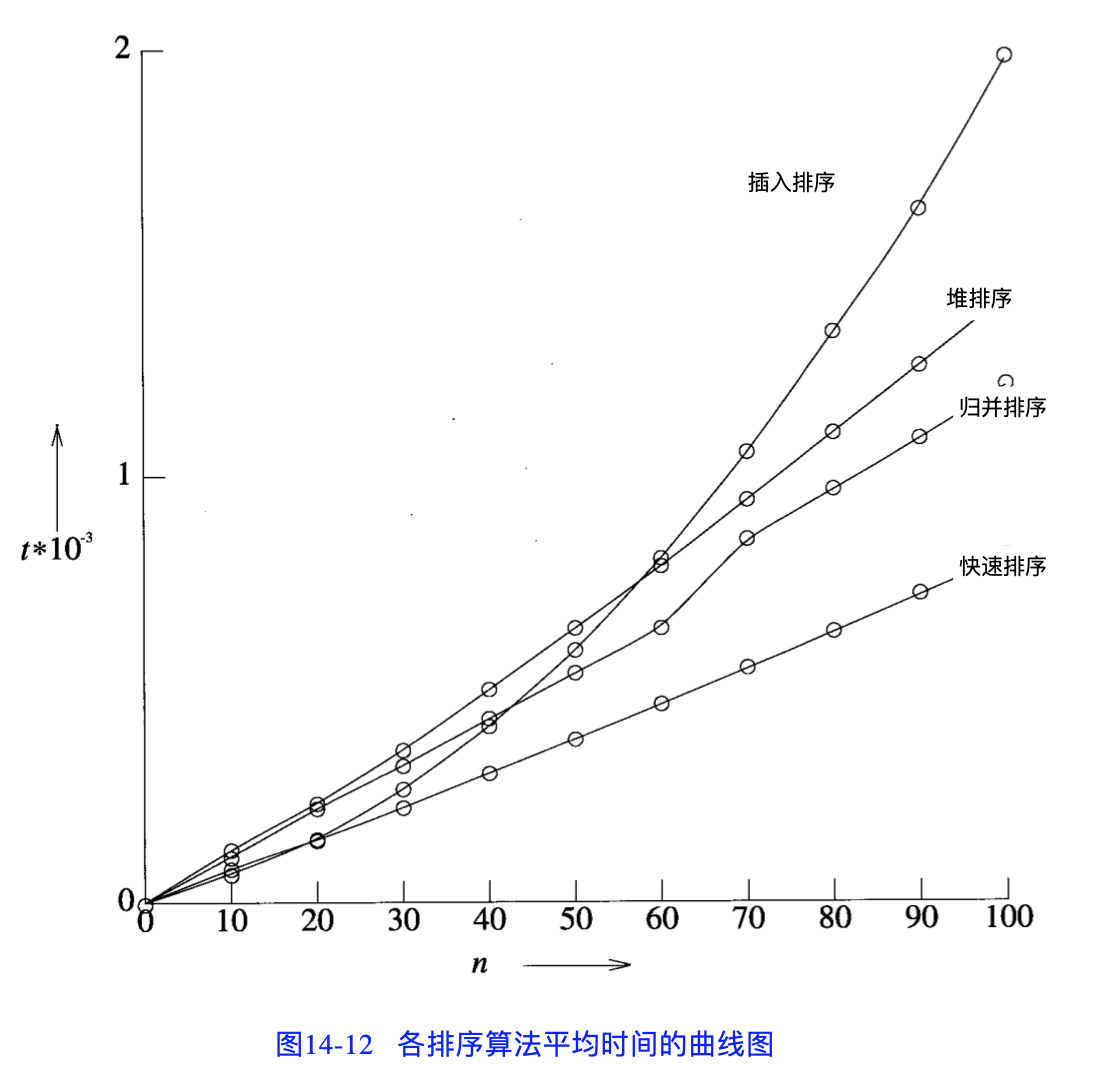
今天将多年前整理的一些排序算法捋一捋。先说个大概。
排序算法通常按照以下标准分类:
1. 依据待排序数列的大小
- 一般而言,好的性能是
,坏的性能是 。 - 对于一次排序,理想的性能是
;然而在平均上总是需要 。
2. 存储器使用量(以及其他计算机资源的使用)
3. 稳定性:指的是某个排序算法会让原本有相同键值的记录维持相对次序。
- 如果一个排序算法是稳定的,当有两个相同键值的记录 R 和 S,且在原本数列中 R 出现在 S 之前,那么在排序过的数列之中,R 也将会在 S 之前。
稳定排序算法
不稳定排序算法
怎么记忆哪些是稳定算法?
- 时间复杂度复杂一些的(高级,包括快排、shell 排序、堆排序 —— 归并排序除外)都不稳定(选择排序也不稳定);
- 时间复杂度简单一些的(低级,包括冒泡、插入、计数、基数)都稳定(归并排序也是稳定的);
- 复杂算法中,归并排序是稳定排序;简单算法中,选择排序不稳定;
- 8 种稳定,4 种不稳定。
比较 v.s. 不比较
基于比较的排序(Comparison Sort):通过对序列中的数据进行比较,确定数据的先后顺序。
包括:
比较排序有着局限性:不能突破
- 简单证明:
个数有 个可能的全排列,即基于比较的排序算法的判定树有 个叶节点,比较次数最少为 (斯特林公式)
相对应的,非比较排序有:
非比较排序的局限性是:对排序元素之间差值的大小有限制。
算法性能
总结了个表格(n 为数据量大小):
| 类别 | 排序方法 | 数据对象 | 稳定性 | 时间复杂度 | 空间复杂度 | ||
|---|---|---|---|---|---|---|---|
| 平均情况 | 最好情况 | 最坏情况 | |||||
| 插入排序 | 直接插入排序 | 数组、链表 | ☑️ | O(n2) | O(n) | O(n2) | O(1) |
| shell 排序 | 数组 | ✖️ | O(nlogn) | O(n) | O(nlogn) | O(1) | |
| 选择排序 | 直接选择排序 | 数组 | ✖️ | O(n2) | O(n2) | O(n2) | O(1) |
| 链表 | ☑️ | ||||||
| 堆排序 | 数组 | ✖️ | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | |
| 交换排序 | 冒泡排序 | 数组 | ☑️ | O(n2) | O(n) | O(n2) | O(1) |
| 快速排序 | 数组 | ✖️ | O(nlogn) | O(nlogn) | O(n2) | O(logn) | |
| 归并排序 | 数组、链表 | ☑️ | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | |
| 桶排序 | 数组、链表 | ☑️ | O(n+k) | O(n+k) | O(n2) | O(n+k) | |
| 基数排序 | 数组 | ☑️ | O(nk) | O(nk) | O(nk) | O(n+k) | |
| 计数排序 | 数组、链表 | ☑️ | O(n+k) | O(n+k) | O(n+k) | O(n+k) | |
注:对于非比较排序来说,k 为“桶”的个数。
再上个教材的图: