AVL 树是最先被发明的自平衡二叉查找树。
背景
AVL 树是由 Adelson-Velskii 和 Landis 共同提出的一种数据结构,因此得名。
所谓的“平衡”,指的是:
- 左右子树的高度差小于等于 1;
- 其每一个子树均为平衡二叉树。
为了保证二叉树的平衡,AVL 树引入了监督和自调节机制:在树的某一部分的不平衡度超过一个阈值时,会触发相应的平衡操作,保证其平衡度在可以接受的范围内。
定义
空的二叉树是 AVL 树。
对于非空二叉树,满足以下条件时为 AVL 树:
- 其左子树和右子树都是 AVL 树
, 和 分别是左子树和右子树的高度 - 即:在 AVL 树中任何节点的两个子树高度差不大于 1
- 这种以高度为平衡条件的树也叫高度平衡树
衍生定义
AVL 搜索树:既是二叉搜索树,也是 AVL 树的一种数据结构。
带索引的 AVL 搜索树:顾名思义。
- 图 1
a)b)和 图 2 是 AVL 树,c)不是 - 图 1
a)不是 AVL 搜索树 - 图 2 是带索引的 AVL 搜索树
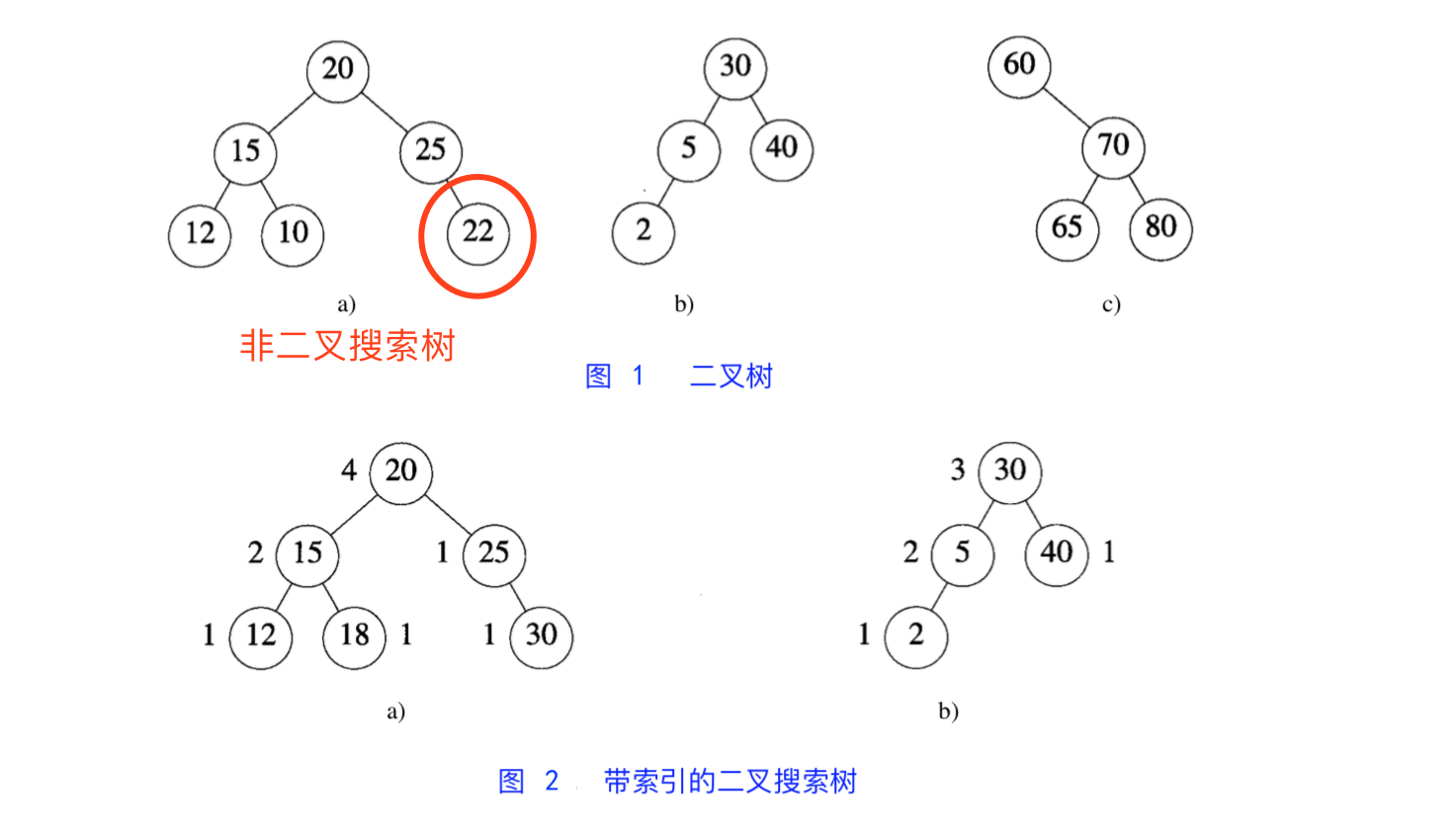
另外,使用 AVL 树描述字典须具备:
- n 个元素(节点)的 AVL 树的高度是
- 对于每一个
,都存在一棵 AVL 树结构与之对应 - 否则完成插入后,一棵 AVL 树将不再是 AVL 树:因为对当前元素数量来说不存在对应的 AVL 树
- 一棵 n 个元素的 AVL 搜索树能在
的时间内完成搜索 - 往一棵 n 元素的 AVL 搜索树中插入一个新元素,可得到一棵 n+1 元素的 AVL 树,该插入过程可在
完成 - 从一棵 n 元素的 AVL 搜索树中删除一个元素,可得到一棵 n-1 元素的 AVL 树,该删除过程可在
完成
注:4. 包含了 2.
由此可得:
- AVL 树的查找、插入和删除操作在平均和最坏情况下都是
。
数据结构描述
我们一般使用链表去描述 AVL 树。
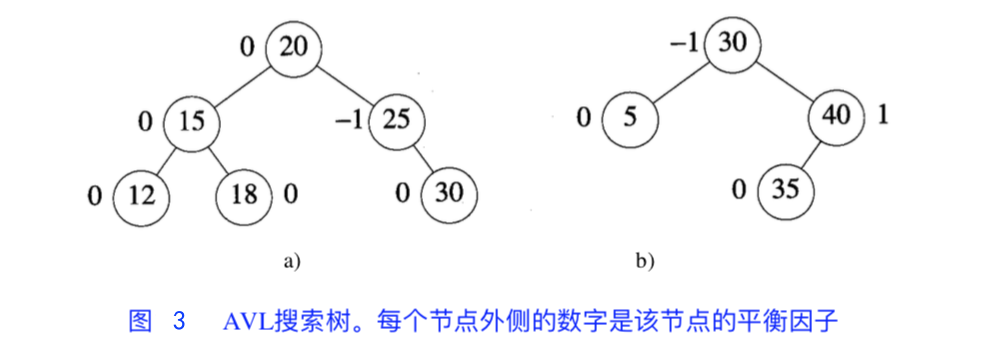
为描述插入和删除操作给树带来的影响,我们为每个节点增加一个平衡因子 bf 的描述:
结合 AVL 树的定义我们可知:
- 平衡因子 1、0、-1 的节点会被认为是平衡的,而 2 或者 -2 被认为是不平衡的,需要重新平衡;
- 因此增加或删除节点,可能需通过一次或者多次树旋转来重新平衡这个树。
树的高度
设
- 最坏情况:根节点两棵子树一棵高度是 h-1,另一棵是 h-2,都是 AVL 树
- 满足:
(与斐波那契数列相似) - 也可:
- 由斐波那契定理:
,其中 ,可得:
- 满足:
如果树中有 n 个节点,那么树的最大高度是:
确定搜索树的高度总为
搜索
可以参照二叉搜索树的搜索算法,时间为
插入
直接使用二叉搜索树的插入算法,得到的可能不是 AVL 树。
存在以下情况:
- 不平衡树中的平衡因子的值限于 -2,-1,0,1,2;
- 平衡因子为 2 的节点在插入前的平衡因子为 1;与此类似,平衡因子为 -2 的,插入前为 -1;
- 从根到新插入节点的路径上,只有途径的节点的平衡因子在插入后会被改变;
- 设 A 是新插入节点最近的祖先,平衡因子为 -2 或 2,那插入前在从 A 到新插入节点的路径上,所有节点的平衡因子为 0。
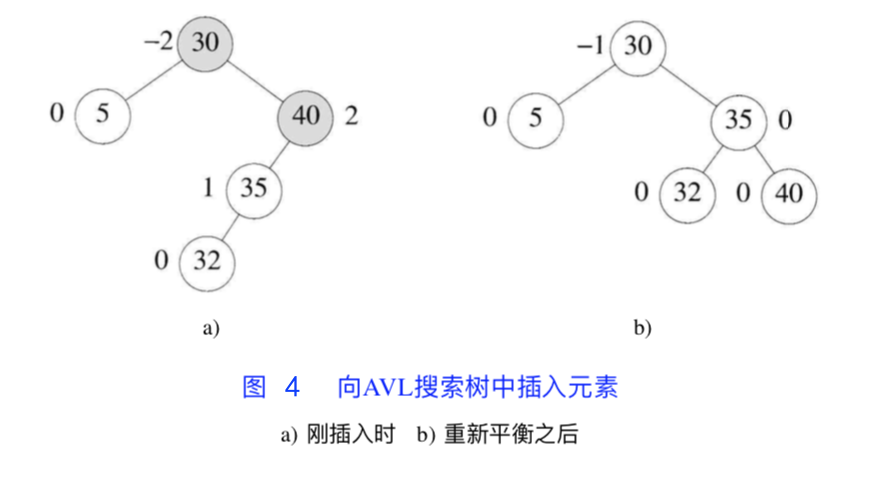
如上图所示:往图 3 b) 插入节点 32 得到图 4 a) 。观察节点 40,其平衡因子 bf 在插入前为 1,插入后为 2,即 A 为值为 40 的节点。
如往图 3 a) 插入节点 26、28、50 或 72,则 A 为值为 25 的节点;
如往图 3 a) 插入节点 10、14、16 或 19,则不存在这样的 A。
如果存在上述的节点 A,说明 AVL 树处于不平衡状态。
不平衡状态分为 L 型不平衡(新插入节点在 A 左子树)或 R 型不平衡(新插入节点在 A 右子树)两个类别,细分则有:
- LL 型不平衡(新插入节点在 A 左子树的左子树中)
- LR 型不平衡(新插入节点在 A 左子树的右子树中)
- RL 型不平衡(新插入节点在 A 右子树的左子树中)
- RR 型不平衡(新插入节点在 A 右子树的右子树中)
当 A 的 bf 值为 -2 或 2,说明 A 保存新插入节点的子树高度至少为 2,也就是说,A 肯定拥有孙节点。
处理插入后失衡:旋转子树
调整 LL 型不平衡:LL 旋转
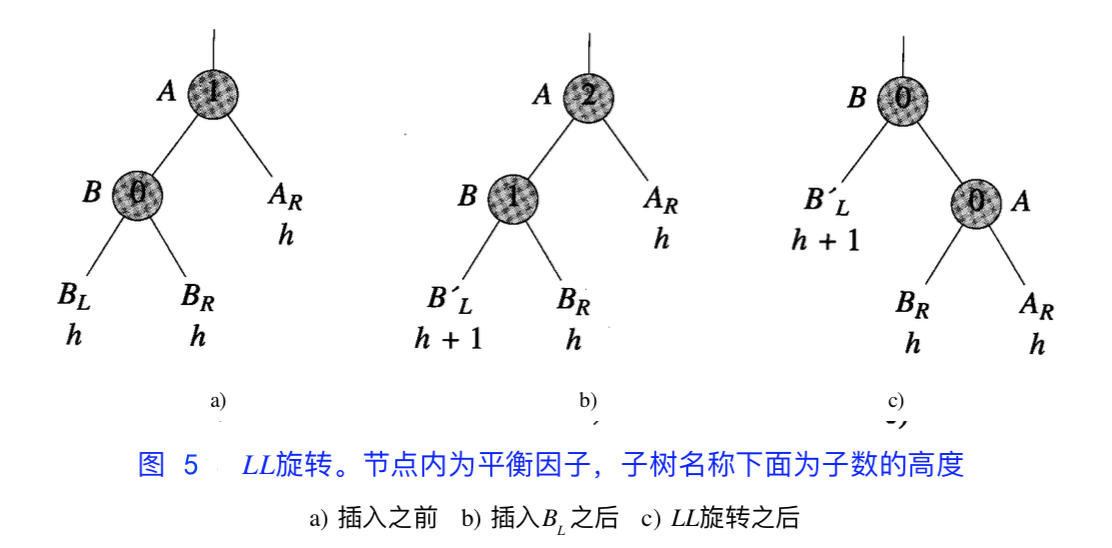
旋转前:
- A 为根节点,B 为左子树根节点
- 新元素比 B 的值小,最终插入到 B 的左子树
, - 插入元素后 B 的左子树比右子树高(
)。
旋转后:
- B 为根节点,A 变成 B 右子树的根节点
- B’L 仍为 B 的左子树,B’R 为 A 的左子树(B < B’R < A),A 的右子树不变
- 从 B 到新插入节点途中的 B’ 的左右节点的平衡因子都将改变,其他节点平衡因子与旋转前一致。
证明其仍为二叉搜索树:
- BR 子树上所有元素原本就比 A 要小:旋转后 B’R 成为 A 左子树,符合要求。
调整 LR 型不平衡:LR 旋转
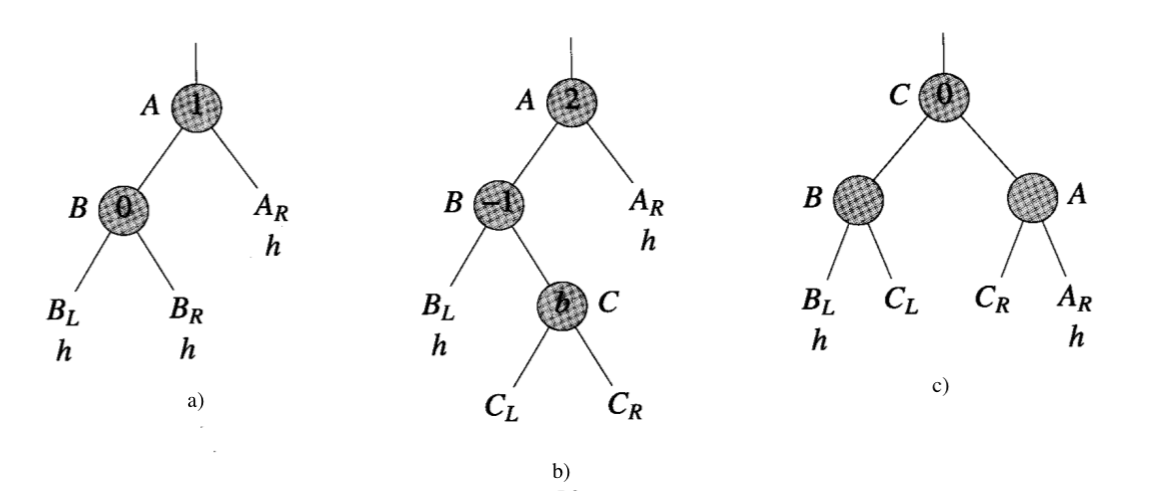
针对于树产生了 LR 不平衡,说明 A 的左子树(记为 B)的右子树(记为 C)肯定存在。
- 此时
, - 注:C 的左右子树(
, )有可能为空。
旋转后,
- 若 b = 0:即
- 因整理前
,可知 - 因此整理后
- 因整理前
- 若 b = 1:即
- 因整理前
,可知 , - 整理后
,
- 因整理前
- 若 b = -1:即
- 因整理前
,可知 , - 整理后
,
- 因整理前
证明其仍为二叉搜索树:
- 旋转前
肯定比节点 大,比 小,因此旋转后形成的根节点和根节点下一层的排列,符合要求 - 旋转前
根节点肯定比 大, 根节点肯定比 小,符合要求。
小结
通过观察上述的旋转过程,我们可以得出:
- LL 和 RR 只需旋转一次,我们称之为单旋转
- LR 和 RL 需要旋转两次,我们称之为双旋转
- 可将 LR 看作是 RR 旋转后的 LL 旋转。
插入算法思路
- 沿着从根节点开始的路径对具有相同键值的元素进行搜索,以找到插入新元素的位置。在此过程中寻找最近的,且平衡因子为 -1 或 1 的节点,令其为 A 节点。如找到相同关键值的元素,则插入失败,以下步骤无需执行;
- 如没有这样的 A 节点:从根节点开始再遍历一次,并修改平衡因子,然后终止;
- 如 bf(A) = 1 并且新节点插入到 A 的右子树中,或 bf(A) = -1 且插入在左子树进行:A 新的平衡因子为 0。此时修改从 A 到新节点途中的平衡因子,然后终止;
- 确定 A 的不平衡类型并执行相应的旋转,在从新子树根节点至新插入节点途中,根据旋转需要修改相应的平衡因子。
删除
同理:直接使用二叉搜索树的删除算法,得到的可能不是 AVL 树。
设被删除的节点的父节点为 q
- 如删除发生在左子树,则 bf(q) 减 1 或者不变;
- 如删除发生在右子树,则 bf(q) 加 1 或者不变。
删除节点之后,如果:
- q 的新的平衡因子是 0,说明 q 子树的高度已减 1,且需要改变它的父节点(如有)和其他某些祖先节点的平衡因子
- q 的新的平衡因子是 -1 或 1:高度与删除前相同,无需改变其祖先的平衡因子值
- q 的新的平衡因子是 -2 或 2:树在 q 节点不平衡
设从 q 到根节点的路径中平衡因子第一个发生改变的节点为 A,此时 A 的平衡因子是 2 或者 -2。
- 如删除在 A 的左子树:L 型不平衡
- 如删除在 A 的右子树:R 型不平衡
- 删除前 bf(A) = 1,删除后 bf(A) = 2,即 A 的右子树高度减 1,属于 R 型不平衡
当删除 A 右子树的节点时,我们将 A 的左子树的根节点记为 B。
如果删除导致 bf(B) = -1,我们将其定义为 R-1 型不平衡。
由此会有以下的不平衡状态定义:
- R-1:A 的左节点 B 的平衡系数为 -1
- R0:A 的左节点 B 的平衡系数为 0
- R1:A 的左节点 B 的平衡系数为 1
- L-1:A 的右节点 B 的平衡系数为 -1
- L0:A 的右节点 B 的平衡系数为 0
- L1:A 的右节点 B 的平衡系数为 1
处理删除后失衡:旋转子树
删除了右子树的节点,左子树平衡因子被改变,左子树需要变化;
对于左子树节点的删除,也是同样的道理。我们这里只介绍 R 型不平衡,对于 L 型不平衡,作镜像处理。
R0 旋转:与插入时的单旋转类似
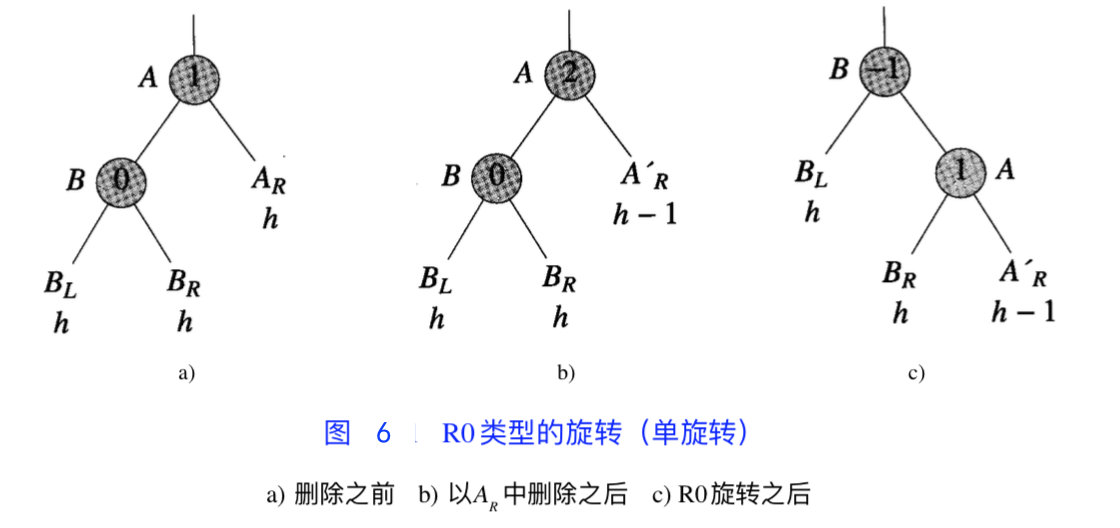
R1 旋转:与插入时的单旋转类似
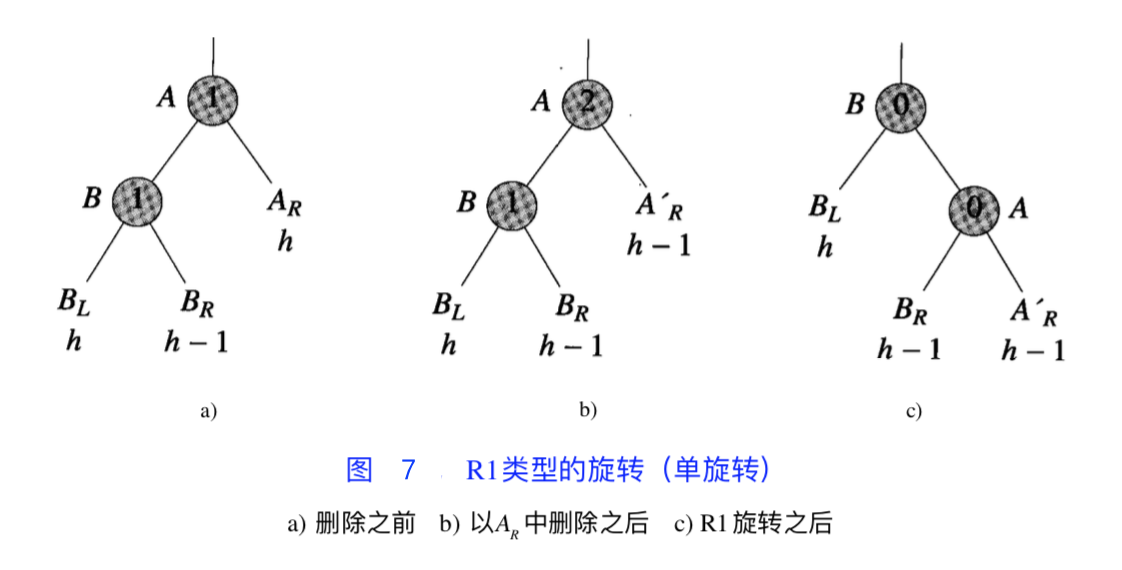
R-1 旋转:与双旋转类似
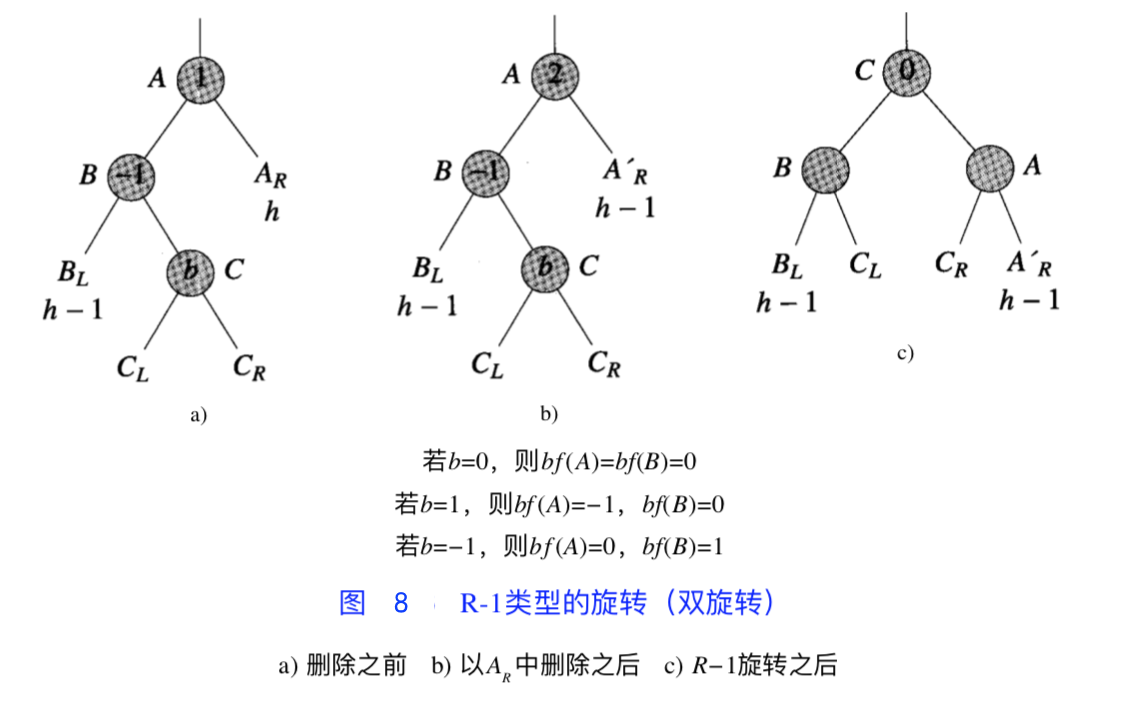
旋转后,
- 若 b = 0:即
- 因整理前
,可知 - 因此整理后
- 因整理前
- 若 b = 1:即
- 因整理前
,可知 , - 整理后
,
- 因整理前
- 若 b = -1:即
- 因整理前
,可知 , - 整理后
,
- 因整理前
删除具体思路
把要删除的节点向下旋转成一个叶节点,接着直接移除该叶节点;
旋转期间最多有