Raymond's Cabin

for sharing thoughts

0%

二叉树

Posted on Valine:

二叉树可能不是计算机世界中最基本的数据结构，但是将它誉为计算机应用中的基石，这个赞誉并不为过。

了解二叉树之前，我们先来理一下“树”的概念。

什么是树

在计算机科学中，线性数据结构和表数据结构一般不适合描述具有层次结构的数据，比如祖先 - 后代、上级 - 下属、整体 - 部分之类的数据。

由此我们引入了一个新类型的非空有限元素的集合：树（tree）

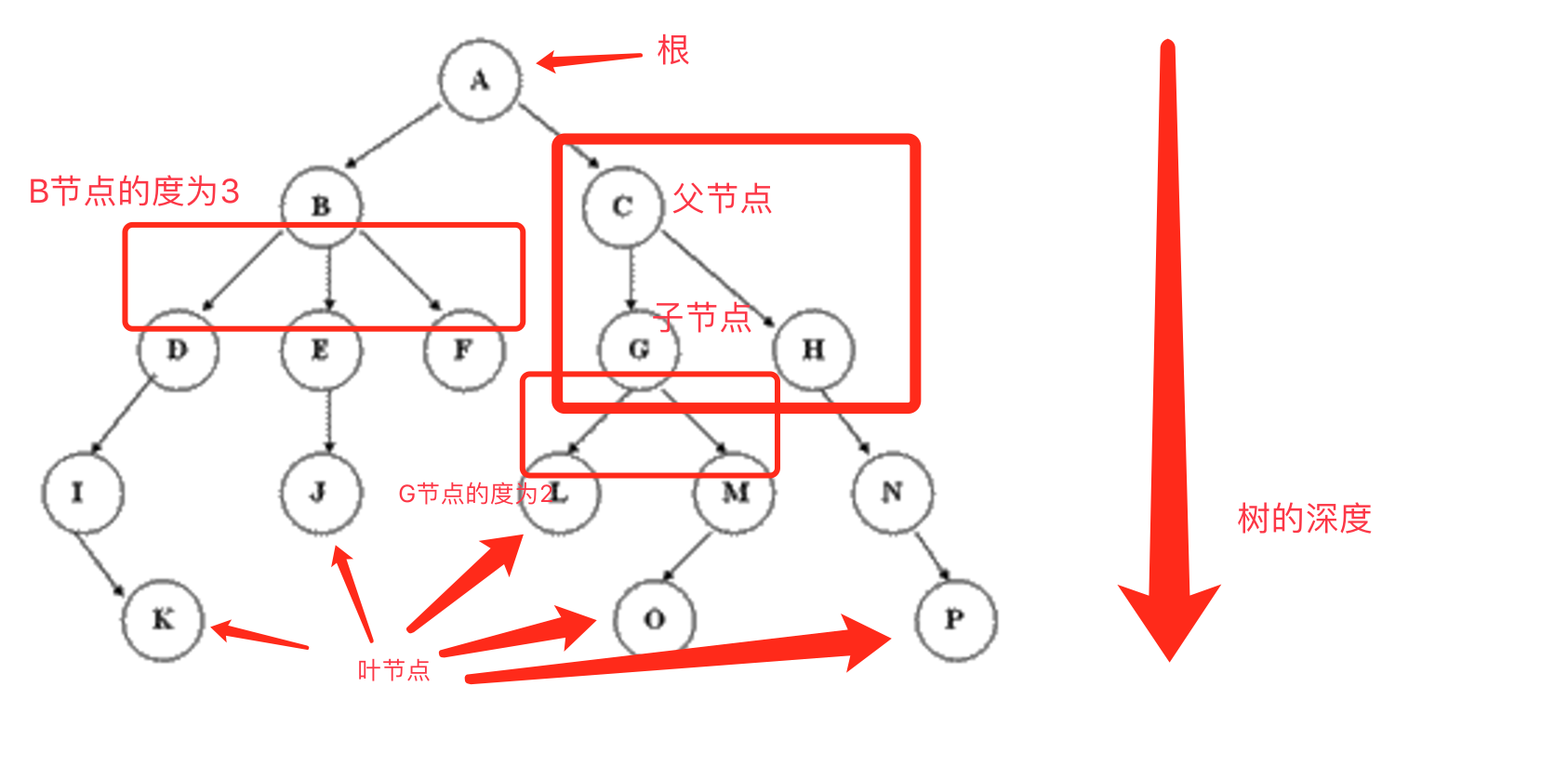
  • 树的最高层元素称为根（root）
  • 余下的非空元素组成该树的子树（subtree）
  • 根在上，树在下
  • 每棵树的末端为树的叶子（leaf node）

一般的树的结构：

树属于抽象数据类型（Abstract Data Type, ADT）。

树的各个概念

父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点。

子节点：一个节点如含有子树，则该子树的根节点称为该节点的子节点。

由此衍生的概念有：

  • 节点的祖先：从根到该节点所经过的分支上的所有节点
  • 子孙：以某节点为根的子树中任一节点都称为该节点的子孙
  • 兄弟节点：具有相同父节点的节点互称为兄弟节点
  • 堂兄弟节点：父节点在同一层的节点互为堂兄弟

节点层次（level）：从根开始定义，根为第一层，根的子节点为第二层……以此类推。

树的高度/深度：树中节点的最大层次。

节点的度（degree of a node）：一个节点含有的子树的棵数

  • 树的度：一棵树中节点的度的最大值
  • 叶节点/终端节点：度为 0 的节点
  • 非终端节点/分支节点：度不为 0 的节点

森林：没有回路的图，也可以看成由 m（m > 0）棵互不相交的树的集合称为森林。

树的种类

按照节点次序可以分为：

  • 无序树：树中任意节点的子节点之间没有顺序关系，也称为自由树
  • 有序树：树中任意节点的子节点之间有顺序关系

有序树中，按照度的数量，可以分为：

  • 二叉树
  • N 叉树


本帖主要介绍二叉树，这也是计算机科学中最常用的树型数据结构。

二叉树

与树不同的是，二叉树可以为空。当二叉树非空时，包括：

  • 根元素
  • 两棵子二叉树，分别叫左子树和右子树

二叉树和树的根本区别：

  • 二叉树可以为空；而树不能为空
  • 二叉树的每个元素恰好有两棵子树（以左、右区分次序，可以为空）；而树中每个元素可以有若干个且无序的子树

二叉树特性

  1. 包含 个元素的二叉树，它的边的数量为
  2. 若二叉树的高度为 ，则该二叉树最少有 h 个元素，最多有 2h - 1 个元素
  3. 包含 n 个元素的二叉树，其高度最大为 n，最小为 （上取整数）
  4. 任意一棵二叉树中，若有 个叶节点， 个度为 2 的节点，则有：
  5. 设完全二叉树中任一元素的序号为 ，则：
    1. 当 i = 1 时，该元素为二叉树的根。若 i > 1，则该元素父节点的序号为 （下取整数）。
    2. 若 2i > n，该元素无左孩子；否则其左孩子的编号为 2i 。
    3. 若 2i + 1 > n，该元素无右孩子；否则其右孩子的编号为 2i + 1 。
  6. 完全二叉树中，度为 1 的节点的数目要不是 1，要不是 0

二叉树的不同形态

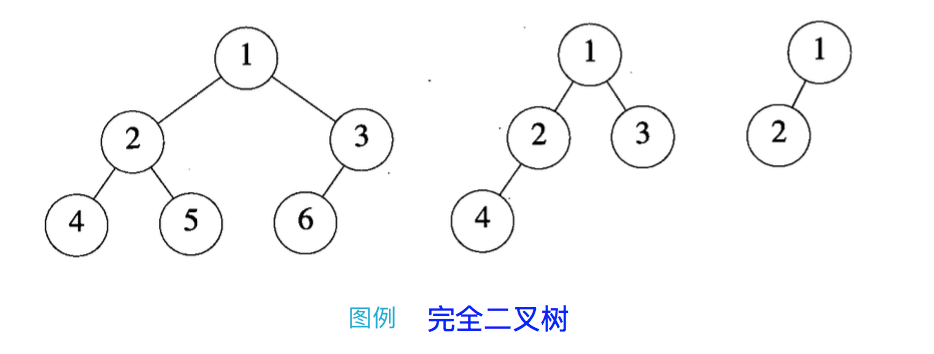
完全二叉树（Complete Binary Tree）

对于一棵深度为 d（d > 1）的二叉树，除了第 d 层（叶子节点那一层）外其他各层节点数目已满，且第 d 层所有节点从左向右连续紧密排列。

我们称这样的二叉树为完全二叉树。

完全二叉树的特性：

  • 左孩子节点位置 = 当前父节点位置 * 2 + 1（从 0 开始）
  • 右孩子节点位置 = 当前父节点位置 * 2 + 2


由完全二叉树衍生出来的：

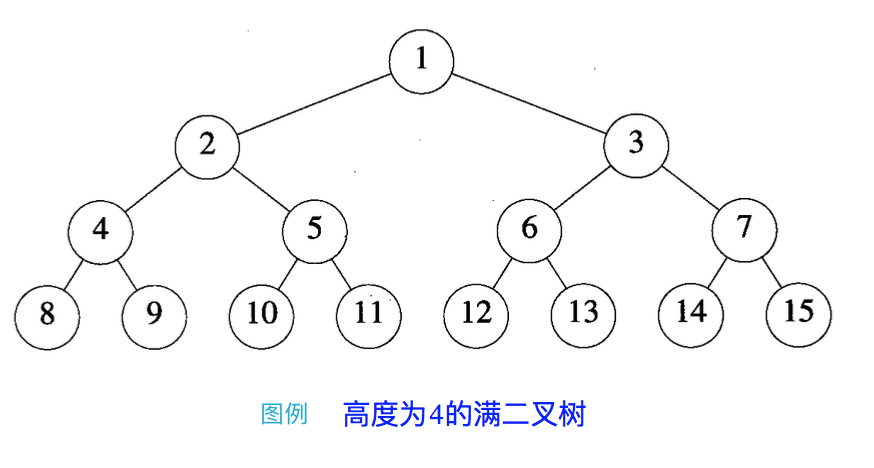
满二叉树（Perfect Binary Tree）完全二叉树去掉第 d 层所有节点之后，所剩下的部分构成一棵满二叉树。

  • 一棵深度为 d - 1 的二叉树含有 2(d - 1) - 1 个元素

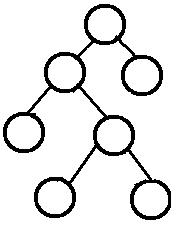
完满二叉树（Full Binary Tree）：除了叶子节点之外的每一个节点都有两个孩子节点。

常用操作

  • 确定高度
  • 确定元素数目
  • 复制单个元素 / 整棵树
  • 打印二叉树
  • 比较两棵二叉树
  • 删除整棵树
  • ……

这些常用操作都可通过遍历二叉树来完成。

数据结构

通常有两种描述二叉树的结构：

1. 公式化描述：利用二叉树的特性 5

  1. 可以将一棵二叉树与其对应的完全二叉树作为比较，逻辑上补全缺少的部分元素
  2. 将二叉树从上到下，从左到右编号后，再存储到数组中

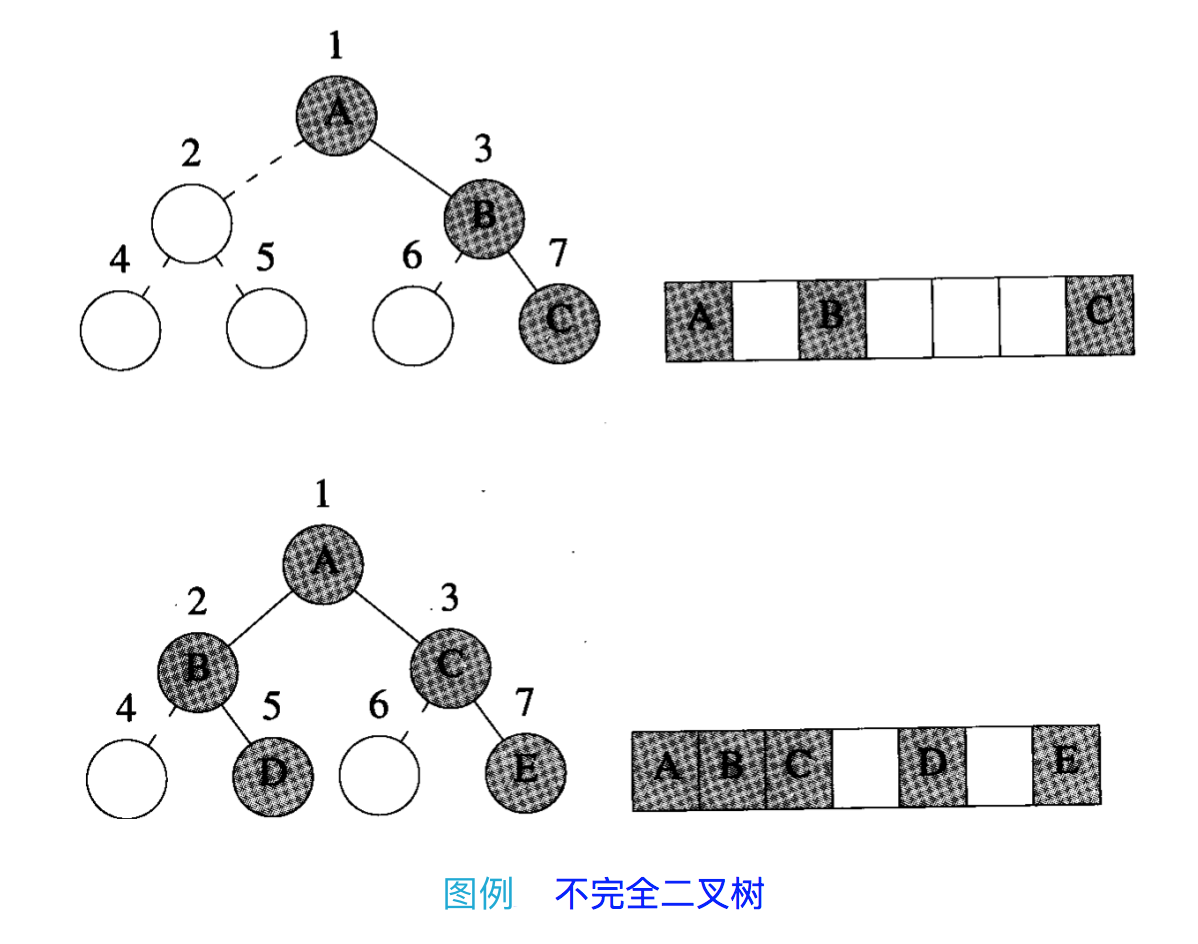
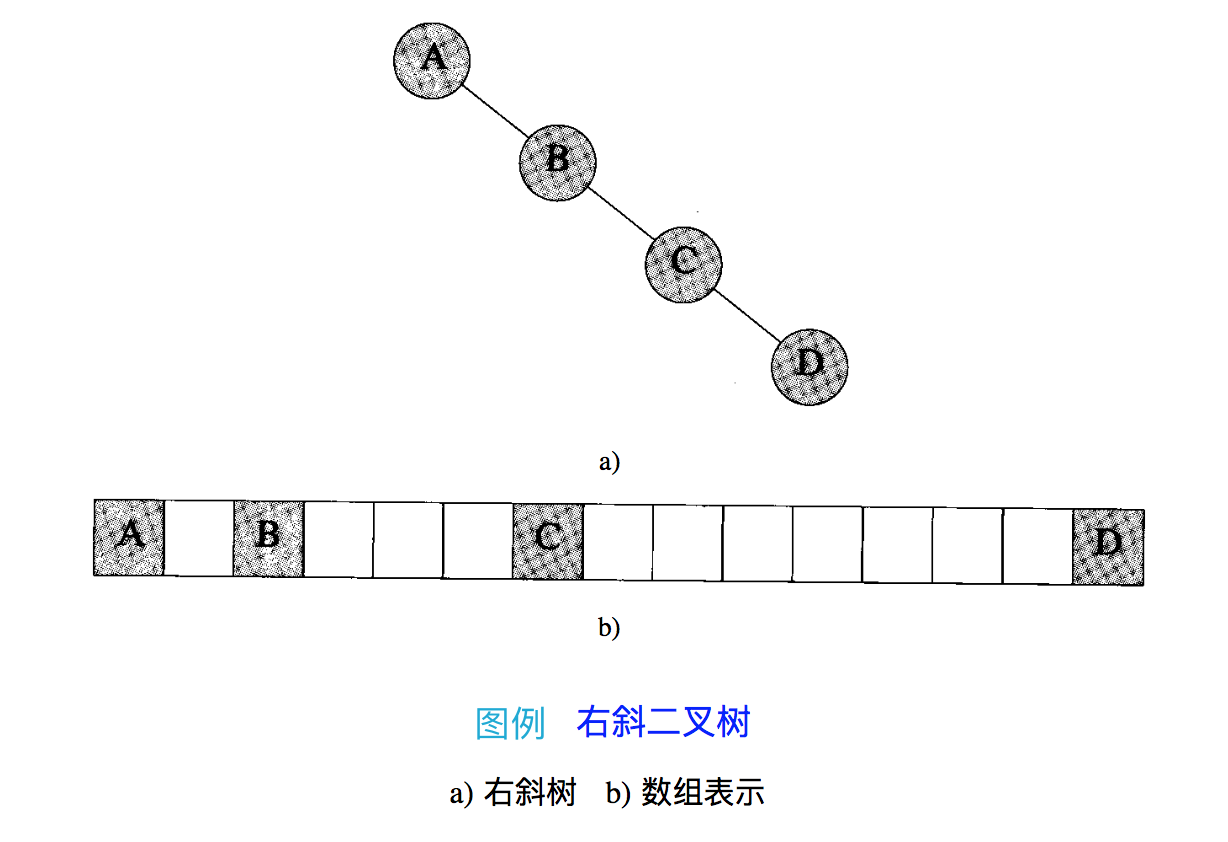
缺点：如果对应的完全二叉树缺少的元素数量很多，就会非常浪费时间和空间，以右斜（right-skewed）二叉树最甚：

2. 链表描述：这是最常用的方法

  • 每个元素使用一个有两个指针域（leftChild, rightChild）和数据域 data 的节点表示
  • 边可以用从父节点指向子节点的指针描述，指针存放于父节点指针域中
  • 拥有 n 个元素的二叉树，会有 个指针域没有值


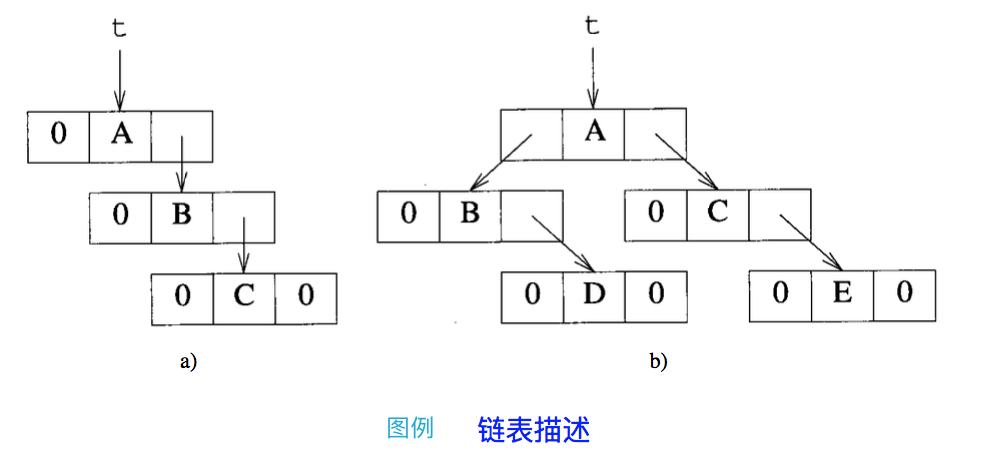
本文我们用链表描述方式来实现二叉树的数据结构。

节点类 BinaryTreeNode

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class BinaryTreeNode {

    private String data = null;

    private BinaryTreeNode leftChild = null;

    private BinaryTreeNode rightChild = null;

    public BinaryTreeNode() {
    }

    public BinaryTreeNode(String data) {
        this.data = data;
        this.leftChild = null;
        this.rightChild = null;
    }

    public String getData() {
        return data;
    }

    public void setData(String data) {
        this.data = data;
    }

    public BinaryTreeNode getLeftChild() {
        return leftChild;
    }

    public void setLeftChild(BinaryTreeNode leftChild) {
        this.leftChild = leftChild;
    }

    public BinaryTreeNode getRightChild() {
        return rightChild;
    }

    public void setRightChild(BinaryTreeNode rightChild) {
        this.rightChild = rightChild;
    }

    @Override
    public String toString() {
        return "Node data: " + getData();
    }
}

二叉树类 BinaryTree

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
import java.util.Deque;
import java.util.LinkedList;
import java.util.Queue;

public class BinaryTree {

    private BinaryTreeNode root;

    public BinaryTree() {
    }

    public BinaryTree(BinaryTreeNode root) {
        this.root = root;
    }

    public BinaryTreeNode getRoot() {
        return root;
    }

    public void setRoot(BinaryTreeNode root) {
        this.root = root;
    }

    public String visit(BinaryTreeNode node) {
        if (node == null || node.getData() == null) {
            return "NULL node";
        }
        return node.toString();
    }

    // 前序遍历
    // 空间复杂度为 Ο(n)，时间复杂度为 Θ(n)
    public void preOrder(BinaryTreeNode node) {
        if (node == null) {
            return;
        }
        visit(node);
        preOrder(node.getLeftChild());
        preOrder(node.getRightChild());
    }

    // 前序遍历非递归实现
    public void preOrderNonRecur(BinaryTreeNode node) {
        if (node == null) {
            return;
        }
        Deque<BinaryTreeNode> stack = new LinkedList<>();
        stack.push(node);
        while (!stack.isEmpty()) {
            node = stack.pop();
            visit(node);
            // 利用栈的 FILO 原理，右子树先入栈，后出栈
            if (node.getRightChild() != null) {
                stack.push(node.getRightChild());
            }
            // 左子树后入栈，先出栈
            if (node.getLeftChild() != null) {
                stack.push(node.getLeftChild());
            }
        }
    }

    // 中序遍历
    // 空间复杂度为 Ο(n)，时间复杂度为 Θ(n)
    public void inOrder(BinaryTreeNode node) {
        if (node == null) {
            return;
        }
        inOrder(node.getLeftChild());
        visit(node);
        inOrder(node.getRightChild());
    }

    // 中序遍历非递归实现
    public void inOrderNonRecur(BinaryTreeNode node) {
        if (node == null) {
            return;
        }
        Deque<BinaryTreeNode> stack = new LinkedList<>();
        while (node != null || !stack.isEmpty()) {
            // 一直将左子树的左节点推进栈
            while (node != null) {
                stack.push(node);
                node = node.getLeftChild();
            }
            // 左节点操作完毕
            if (!stack.isEmpty()) {
                node = stack.pop();
                visit(node);
                node = node.getRightChild();  // 再推右子树
            }
        }
    }

    // 后序遍历
    // 空间复杂度为 Ο(n)，时间复杂度为 Θ(n)
    public void postOrder(BinaryTreeNode node) {
        if (node == null) {
            return;
        }
        postOrder(node.getLeftChild());
        postOrder(node.getRightChild());
        visit(node);
    }

    // 后序遍历非递归实现
    public void postOrderNonRecur(BinaryTreeNode node) {
        if (node == null) {
            return;
        }
        Deque<BinaryTreeNode> stack = new LinkedList<>();
        BinaryTreeNode prev = null;  // 避免重复遍历节点 -> 右子树再添加的死循环
        while (node != null || !stack.isEmpty()) {
            // 先一直遍历到最左端子树左叶子
            while (node != null) {
                stack.push(node);
                node = node.getLeftChild();
            }
            node = stack.peek();
            if (node.getRightChild() == null || node.getRightChild() == prev) {
                node = stack.pop();
                visit(node);
                prev = node;
                node = null;
            } else {
                node = node.getRightChild();
            }
        }
    }

    // 以上的顺序遍历都是 DFS


    // 逐层遍历（BFS）
    // 时间复杂度为 Θ(n)
    public void levelOrder(BinaryTreeNode node) {
        if (node == null) {
            return;
        }
        Queue<BinaryTreeNode> queue = new LinkedList<>();
        queue.add(node);
        while (!queue.isEmpty()) {
            BinaryTreeNode removed = queue.poll();
            visit(removed);
            if (removed.getLeftChild() != null) {
                queue.add(removed.getLeftChild());
            }
            if (removed.getRightChild() != null) {
                queue.add(removed.getRightChild());
            }
        }
    }


    // 上述操作，对于满二叉树所需的空间为 Θ(n)


    // 返回二叉树高度
    // 时间复杂度为 Θ(n)
    public int height(BinaryTreeNode node) {
        return node == null ? 0 :
            1 + Math.max(height(node.getLeftChild()), height(node.getRightChild()));
    }

    public int height() {
        return height(root);
    }

    // 确定二叉树元素数目
    // 此处实现基于前序遍历
    public int count(BinaryTreeNode node) {
        return node == null ? 0 :
            1 + Math.addExtract(count(node.getLeftChild()), count(node.getRightChild()));
    }

    // 比较二叉树
    public boolean compare(BinaryTreeNode p, BinaryTreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        if (p == null || q == null) {
            return false;
        }
        if (!p.getData().equals(q.getData())) {
            return false;
        }
        return compare(p.getLeftChild(), q.getLeftChild())
                && compare(p.getRightChild(), q.getRightChild());
    }

    // 复制二叉树
    // 此处实现基于前序遍历
    public BinaryTreeNode copy(BinaryTreeNode node) {
        if (node == null) {
            return node;
        }
        BinaryTreeNode copied = new BinaryTreeNode(node.getData());
        copied.setLeftChild(copy(node.getLeftChild()));
        copied.setRightChild(copy(node.getRightChild()));
        return copied;
    }

    public void clear(BinaryTreeNode node) {
        if (node == null) {
            return;
        }
        clear(node.getLeftChild());
        clear(node.getRightChild());
        node = null;
    }

    public void clear() {
        clear(root);
    }

    public boolean isEmpty() {
        return root == null;
    }
}

应用：数学表达树

  • 前序遍历：前缀（prefix）表达式
  • 中序遍历：中缀（infix）表达式
  • 后序遍历：后缀（postfix）表达式

例子：

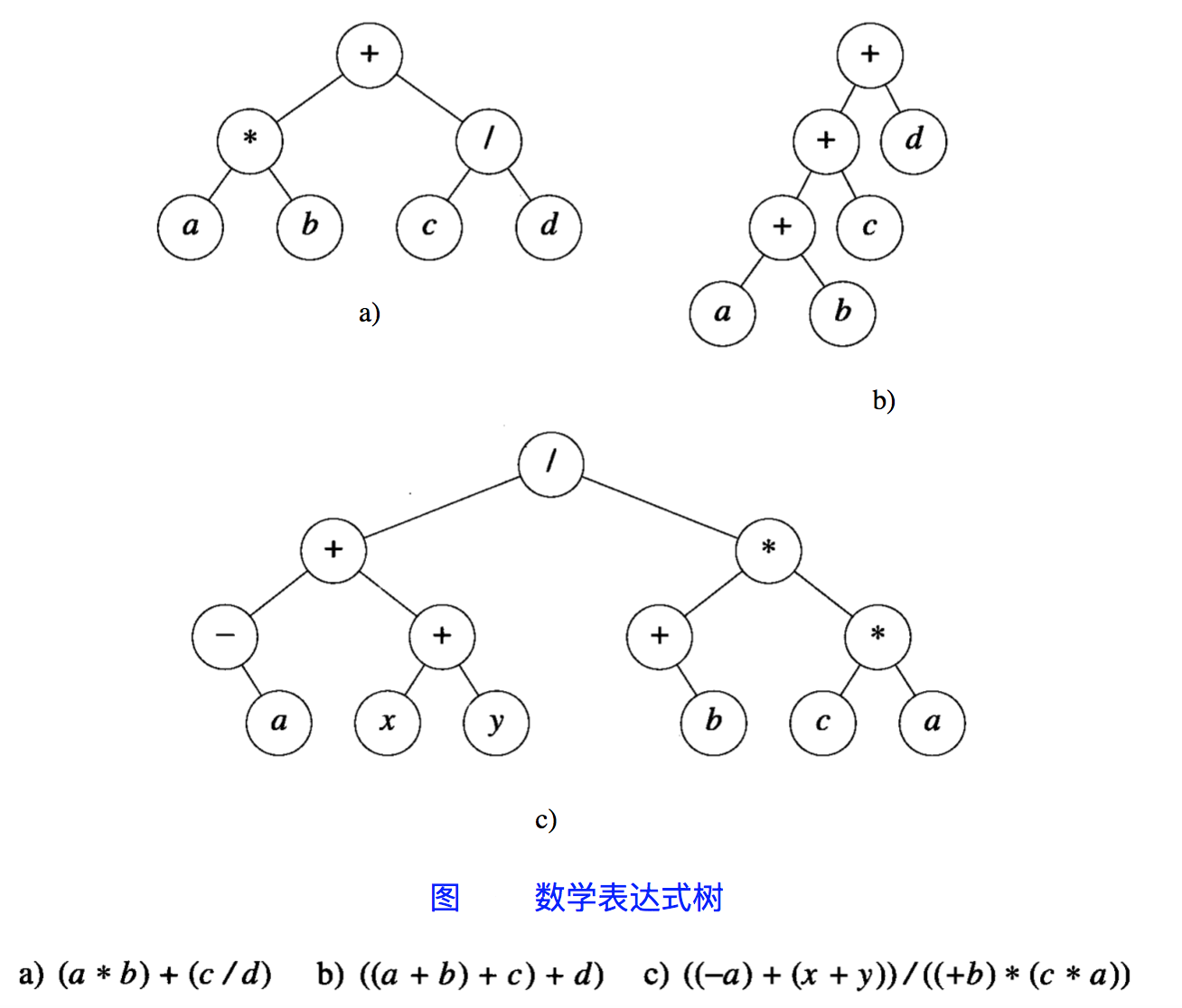
遍历结果：

树 a) b) c)
前序 +*ab/cd +++abcd /+-a+xy+bca
中序 a*b+c/d a+b+c+d -a+x+y/+bca
后序 ab*cd/+ ab+c+d+ a-xy++b+ca**/

应用：二叉搜索树（Binary Search Tree）