B 树

AVL 树和红-黑树在内存中能够保持很好的性能，但不适用于规模大的字典，如外部字典或文件等用途。

因此我们采用度数更高的搜索树改善性能。

背景：ISAM

Indexed Sequential Access Method，索引顺序访问方法，本质上是公式化描述。

• 将可用的磁盘空间划分成多块（磁盘空间最小单位），每个块包含 m 个元素（m 通常较大）
• 字典元素以升序存储在块中
• 索引存储了每个块中关键值的最大值，即索引的关键值数量与块数相同
  • 因此访问关键值 k 的时候，可以通过二分法，在索引中寻找包含相应元素的块，再在相应的块中寻找。

背景：m 叉搜索树

m-way search tree，可以是一棵空树。

如果树非空，则需要满足：

1. 在相应的扩充搜索树中（用外部节点替换零指针），每个内部节点最多有 m 个子女及 1 ~ 个元素（外部节点不含元素和子女）
2. 每个包含 p 个元素的节点，有 p+1 个子女
3. 对于含 p 个元素的任意节点
   1. 设 , …, 为这些元素的关键值，且顺序排列
   2. 设 , , …, 是该节点的 p+1 个孩子，则：
   3. 以 为根的子树中的关键值小于
   4. 以 为根的子树中的关键值大于
   5. 以 为根的子树中的关键值大于 ，小于 （）

如下例图所示：

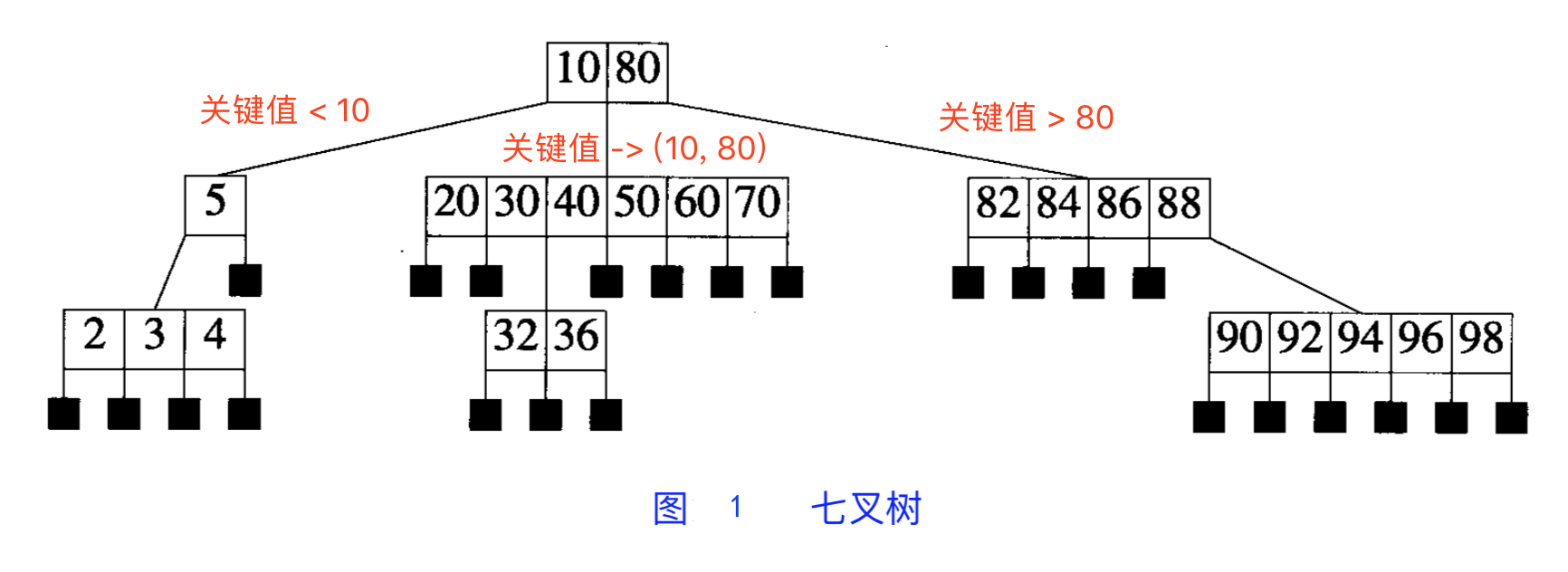
• 查找、搜索按照正常的方法进行
• 删除需要从非空相邻子树挑选替换元素

高度

对于一棵高度为 h 的 m 叉搜索树来说：

• 最少有 个元素：每层一个节点，每个节点一个元素
• 最多有 个元素
  • 从 1 到 h - 1 层每个节点都含有 m 个孩子，且第 h 层的节点没有孩子
  • 共 个节点
  • 每个节点最多包含 个元素，因此最多一共 个元素

即：一棵包含 n 个元素的 m 叉树高度在 到 之间。

m 序 B 树

B-Tree of order m，是一棵 m 叉搜索树。

如果树非空，则相应的扩充搜索树应该满足：

1. 根节点至少有两个孩子
2. 除根节点外，所有内部节点至少有 个孩子
3. 每个节点元素从小到大排列，即左小右大
4. 所有外部节点在同一层，即根节点到每个叶子节点的长度都相同。

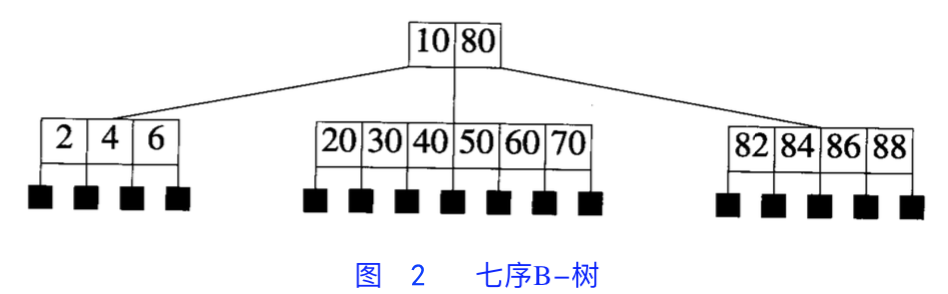
三序 B 树（2-3 树）

即 m = 3 的 B 树，内部节点可以有两个子节点和 1 个数据元素、或 3 个孩子节点和两个数据元素，叶子节点有 1 到 2 个数据元素。

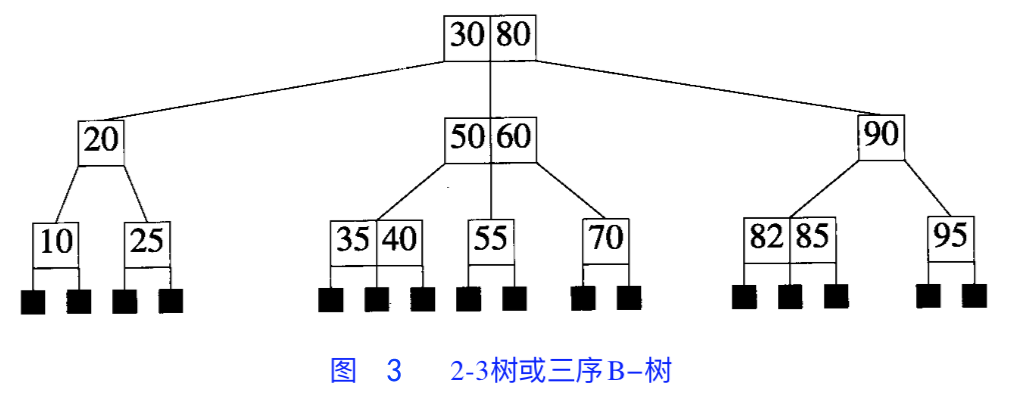
高度

定理：

设 T 是一棵高度为 h 的 m 序 B 树，，n 是 T 中的元素个数，则

证明：

• n 的上限：已证明
• n 的下限：
  • 相应的扩充 B 树的外部节点都在 h+1 层
  • 1, 2, 3, 4, …, h+1 层的节点最小数目是 , , , , …,
  • B 树外部节点最小数为
  • 因外部节点比元素个数多 1：得出下限值
• 由 1 可得 2

因此即使元素数量再多，树的高度也可以很小。
在实际应用中，树的序可以做到很大。

搜索

B 树的搜索算法与 m 叉搜索树的相同，磁盘访问次数最多是 h。

插入

• 首先检查具有相同关键值元素是否存在
  • 如已经存在：不允许重复值，插入失败
• 否则便可将元素插入到树中

当新元素需要插入到饱和节点（超过了规定的 m 值）中时，饱和节点需要被分开。

将饱和节点记为 P：

• 将带有空指针的新元素 e 插入到 P 中，得到一个有 m 个元素和 m+1 个孩子的溢出节点

• 以序列表示如下：

  （ 是元素， 是孩子指针）

我们从 处分开节点（已知 ），将左边元素保留在 P 中，右边元素分到新的节点 Q 中：

$$P: d-1, c_0, (e_1, c_1), ..., (e_{d-1}, c_{d-1})$$ $$Q: m-d, c_d, (e_{d+1}, c_{d+1}), ..., (e_m, c_m)$$

与此同时：

• 被插入到 P 的父节点中
• 要保证 P 和 Q 的孩子数量至少为 d

当操作引起 s 个节点分裂时：

• 磁盘访问次数 = （读取搜索路径上的节点） （回写两个分裂出的新节点）（回写新的根节点或插入后没有导致分裂的节点）
• 最多可达

删除

分两种情况讨论：

当被删除的元素在叶节点时，其孩子均为外部节点的节点：

• 被删除元素在一个包含多于最少数目元素（又是树叶又是根节点：1；不是：⌈m/2⌉-1）的节点：将修改后的节点写回
• 被删除元素在非根且元素数量为最小值的节点：用其最相邻的左或右兄弟的元素替换
  • 将该元素往上移至其父节点，父节点被牵涉到的元素往下移动
• 最相邻的兄弟不含额外的元素：将两个兄弟（自己，不含额外元素的最相邻兄弟）和父节点中介于两兄弟之间的元素合并
• 合并会减少父节点个数：需要检查父节点是否满足要求，并检查父节点相邻的兄弟
  • 要么从中取一个元素，要么与它合并
  • …
  • 由此类推，最坏情况是一直回溯到根节点：变成空节点被抛弃，高度减 1

当被删除的元素在非叶节点：

• 转化为 1.：既可以用左相邻子树中最大元素，也可以用右相邻子树最小元素替换被删除元素

最坏情况的磁盘被访问次数：3h

1. 找到包含被删除元素需要 h 次读访问
2. 获得第 2 到 h 层的最相邻兄弟需要 h-1 次读访问
3. 在第 3 至 h 层的合并需要 h-2 次写访问
4. 对修改过的根节点和第 2 层的两个节点进行 3 次写访问

小结

• B 树：每个节点存储 M/2 到 M 个关键字，非叶子节点存储指向关键字范围的子节点
  • 所有关键字在整棵树出现，且只出现一次，没有冗余
  • 因此非叶子节点可以命中搜索记录
• B+ 树：在 B 树基础上，为叶子节点增加链表指针
  • 所有关键字（值）在叶子节点中完整出现
  • 非叶子节点作为叶子节点的索引，与叶子节点是有冗余的
  • 搜索结果总是要到叶子节点才命中
• B* 树：在 B+ 树基础上，为非叶子节点也增加链表指针

应用：直方图，关系型数据库存储